Tài liệu Giáo viên
Lớp 2Lớp 2 - kết nối tri thức
Lớp 2 - Chân trời sáng tạo
Lớp 2 - Cánh diều
Tài liệu Giáo viên
Lớp 3Lớp 3 - kết nối tri thức
Lớp 3 - Chân trời sáng sủa tạo
Lớp 3 - Cánh diều
Tài liệu Giáo viên
Tài liệu Giáo viên
Lớp 4Lớp 4 - kết nối tri thức
Lớp 4 - Chân trời sáng tạo
Lớp 4 - Cánh diều
Tiếng Anh lớp 4
Tài liệu Giáo viên
Lớp 5Sách giáo khoa
Sách/Vở bài bác tập
Tài liệu Giáo viên
Lớp 6Lớp 6 - liên kết tri thức
Lớp 6 - Chân trời sáng sủa tạo
Lớp 6 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 7Lớp 7 - kết nối tri thức
Lớp 7 - Chân trời sáng tạo
Lớp 7 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 8Lớp 8 - kết nối tri thức
Lớp 8 - Chân trời sáng sủa tạo
Lớp 8 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 9Sách giáo khoa
Sách/Vở bài xích tập
Tài liệu Giáo viên
Lớp 10Lớp 10 - liên kết tri thức
Lớp 10 - Chân trời sáng tạo
Lớp 10 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 11Lớp 11 - kết nối tri thức
Lớp 11 - Chân trời sáng sủa tạo
Lớp 11 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 12Sách giáo khoa
Sách/Vở bài bác tập
Tài liệu Giáo viên
cô giáoLớp 1
Lớp 2
Lớp 3
Lớp 4
Lớp 5
Lớp 6
Lớp 7
Lớp 8
Lớp 9
Lớp 10
Lớp 11
Lớp 12

Chuyên đề Toán 9Chuyên đề: Hệ nhì phương trình bậc nhất hai ẩn
Chuyên đề: Phương trình bậc hai một ẩn số
Chuyên đề: Hệ thức lượng trong tam giác vuông
Chuyên đề: Đường tròn
Chuyên đề: Góc với đường tròn
Chuyên đề: hình tròn - Hình Nón - Hình Cầu
Dạng bài bác tập Tìm quý hiếm của thay đổi để biểu thức có giá trị nguyên cực hay
Trang trước
Trang sau
Cách giải bài bác tập Tìm quý giá của biến đổi để biểu thức có mức giá trị nguyên lớp 9 với phương thức giải chi tiết và bài tập đa dạng chủng loại giúp học viên ôn tập, biết cách làm bài bác tập Tìm cực hiếm của biến hóa để biểu thức có giá trị nguyên.
Bạn đang xem: Giá trị nguyên
Dạng bài tập Tìm giá trị của phát triển thành để biểu thức có mức giá trị nguyên rất hay
Phương pháp giải
a) kiếm tìm x nguyên nhằm biểu thức A =
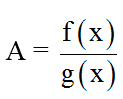
Bước 1. Tách bóc A thành dạng
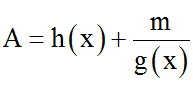
trong kia h(x) là 1 trong những biểu thức nguyên lúc x nguyên, m là nguyên.
Bước 2: A nguyên ⇔
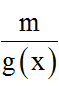
Bước 3. Cùng với mỗi quý giá của g(x), tìm x khớp ứng và kết luận.
b) search x nhằm biểu thức A nguyên (Sử dụng cách thức kẹp).
Bước 1: Áp dụng các bất đẳng thức nhằm tìm nhì số m, M làm thế nào cho m
Ví dụ minh họa
Ví dụ 1: với mức giá trị nguyên làm sao của x thì biểu thức
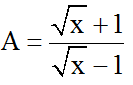
Hướng dẫn giải:
Điều kiện xác định: x ≥ 0; x ≠ 1 .
Ta có:
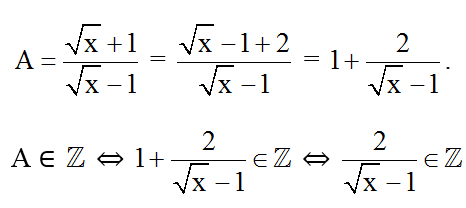
⇔ √x - 1 ∈ Ư(2) = -2; -1; 1; 2
Ta tất cả bảng sau:
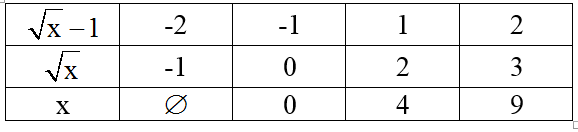
Vậy cùng với x ∈ 0; 4; 9 thì biểu thức A đạt quý giá nguyên.
Ví dụ 2: Tìm quý giá nguyên của x nhằm biểu thức
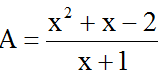
Hướng dẫn giải:
Đkxđ: x ≠ -1.
Ta có:
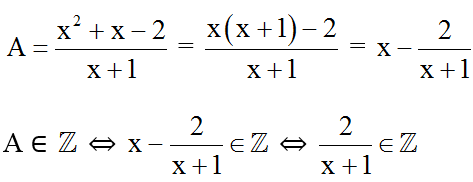
⇔ x + 1 ∈ Ư(2) = -2; -1; 1; 2
⇔ x ∈ -3; -2; 0; 1.
Vậy cùng với x ∈ -3; -2; 0; 1 thì biểu thức A nguyên.
Ví dụ 3: tra cứu x nhằm biểu thức
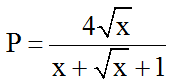
Hướng dẫn giải:
Đkxđ: x ≥ 0.
Ta có:
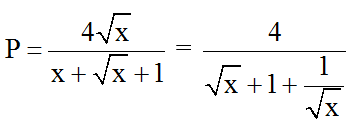
Ta có:
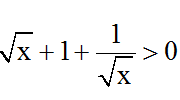
⇒
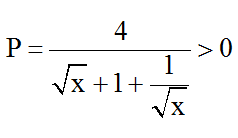
Áp dụng bất đẳng thức Cô-si ta có:
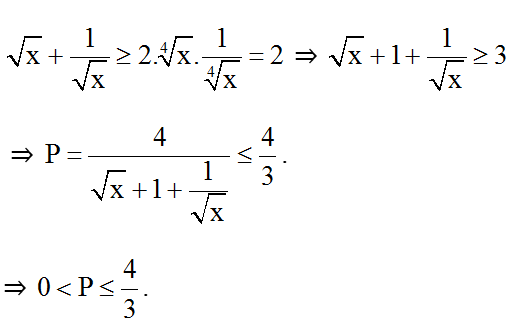
P đạt quý hiếm nguyên ⇔ p = 1
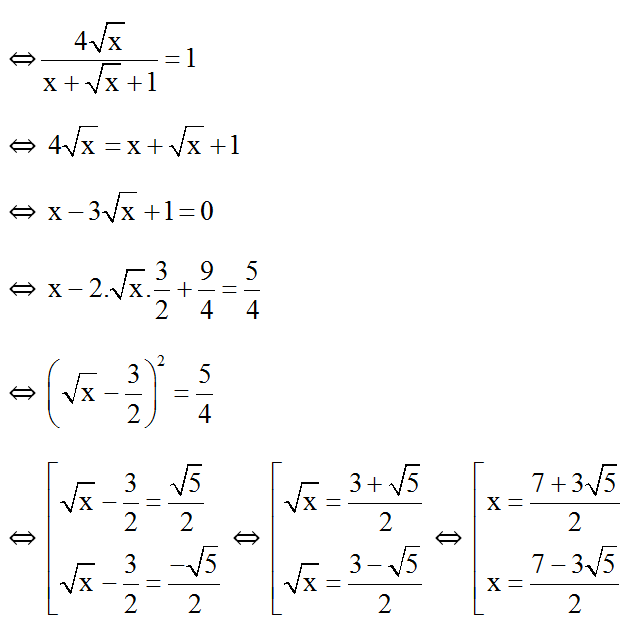
Vậy cùng với
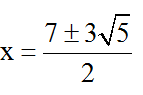
Bài tập trắc nghiệm từ bỏ luyện
Bài 1: giá trị nào của x dưới đây không tạo cho biểu thức
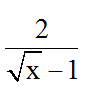
A. 1/4 B. 4C. 2D. 0.
Hiển thị đáp ánĐáp án: C
Bài 2: có bao nhiêu quý giá nguyên của x để biểu thức
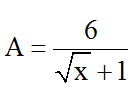
A. 3B. 4C. 6D. 8
Hiển thị đáp ánĐáp án: B
Bài 3: Có tất cả bao nhiêu quý giá nguyên của x để biểu thức
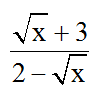
A. 2B. 3C. 4D. 5
Hiển thị đáp ánBài 4: Với toàn bộ các số nguyên x, quý giá nguyên lớn nhất của biểu thức
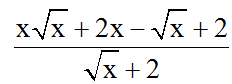
A. 1B. 2C. 3D. 4
Hiển thị đáp ánĐáp án: D
Bài 5: tất cả bao nhiêu giá trị của x nhằm biểu thức
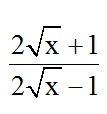
A. 2B. Vô số
C. 3D. 1
Đáp án: B
Bài 6: Tìm các giá trị nguyên của x để những biểu thức sau đây nguyên:
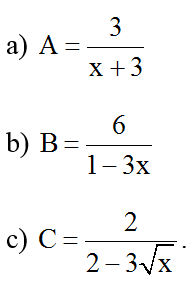
Hướng dẫn giải:
a) Đkxđ: x ≠ -3.
A ∈ Z ⇔ ⇔ x + 3 ∈ Ư(3) = -3; -1; 1; 3 ⇔ x ∈ -6; -4; -2; 0
b) Đkxđ: x ≠ 1/3 .
B ∈ Z ⇔
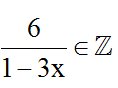
Ta gồm bảng:

Trong các giá trị trên, chỉ gồm x = 1 hoặc x = 0 thỏa mãn x nguyên.
Vậy x = 0 hoặc x = 1.
c)
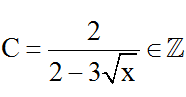
Ta bao gồm bảng sau:
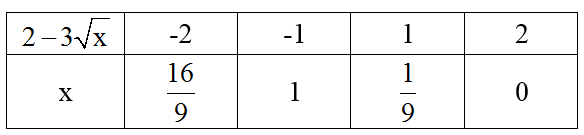
Trong những giá trị bên trên chỉ bao gồm x = 1 hoặc x = 0 thỏa mãn.
Vậy x = 0 hoặc x = 1.
Bài 7: Tìm những giá trị nguyên của x để những biểu thức dưới đây nguyên:

Hướng dẫn giải:
a)
Đkxđ: x ≥ 0; x ≠ 4 .
Ta có:
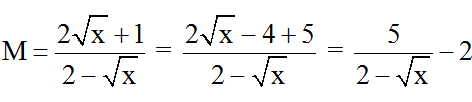
M ∈ Z ⇔
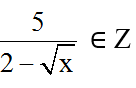
Ta có bảng:

Vậy cùng với x ∈ 49; 9; 1 thì biểu thức M có giá trị nguyên.
b)
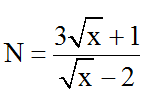
Đkxđ: x ≥ 0 ; x ≠ 4 . Ta có:
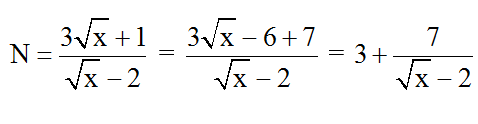
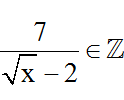
Ta có bảng sau:

Vậy với x ∈ 1; 9; 81 thì biểu thức nhận quý giá nguyên.
Bài 8: Tìm các giá trị của x để các biểu thức
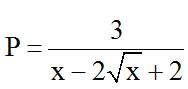
Hướng dẫn giải:
Điều kiện: x ≥ 0 .
Ta có: x - 2√x + 2 = x - 2√x + 1 + 1 = (√x - 1)2 + 1 ≥ 1 > 0
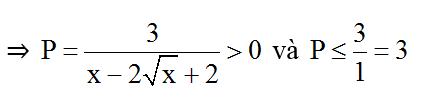
⇒ 0 2 = -3/4 2 = -8/9 0 với tất cả x.
⇒ 0 0; x ≠ 1.
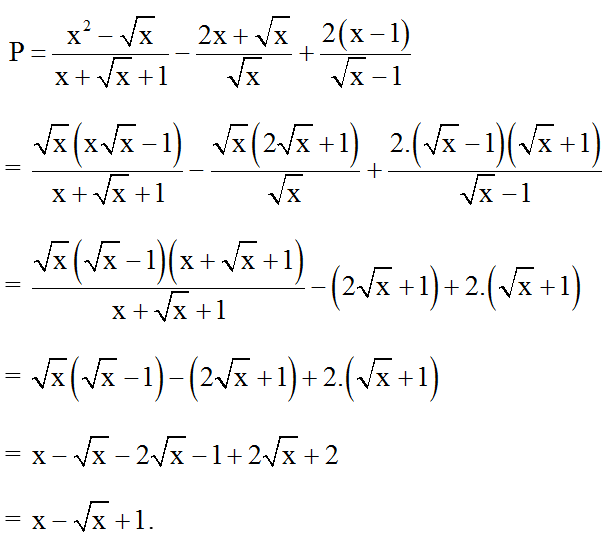
b) Ta có:
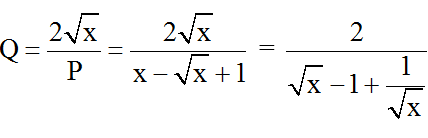
Áp dụng bất đẳng thức Cô-si ta có:
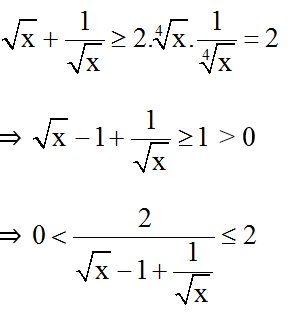
⇒ tốt 0
Bài tập từ luyện
Bài 1. Tìm các giá trị nguyên của x biểu thức sau có mức giá trị nguyêna) 3xx−3;
b) x6x+1;
c) x+5x+3.
Bài 2. tìm x nguyên để những biểu thức sau nguyên
a) x+3x+1;
b) 1x−x+1.
Xem thêm: Có Nên Học Nghề Sửa Chữa Điện Tử Ra Làm Gì? Có Nên Học Nghề Sửa Chữa Điện Tử Không
Bài 3. tra cứu x nguyên nhằm biểu thức M = xx+2−x+4x−4:2x−1x−2x−1x nguyên.
Bài 4. cho biểu thức A = 2xx+3+x+1x−3+3−11x9−xvà B = x−3x+1.
a) Tính quý giá của B khi x = 36;
b) Rút gọn A;
c) kiếm tìm số nguyên x để phường = A.B là số nguyên.
Bài 5. đến biểu thức
P = 1x−1−2xxx−x+x−1:x+xxx+x+x+1+1x+1với x≥0,x≠1
Hãy search x nguyên để p nguyên.
Mục lục các Chuyên đề Toán lớp 9:
Chuyên đề Đại Số 9Chuyên đề Hình học 9Tủ sách VIETJACK shopee luyện thi vào 10 mang đến 2k9 (2024):
Săn shopee rất SALE :
ĐỀ THI, GIÁO ÁN, KHÓA HỌC DÀNH mang lại GIÁO VIÊN VÀ PHỤ HUYNH LỚP 9
Bộ giáo án, bài giảng powerpoint, đề thi giành cho giáo viên với khóa học dành cho phụ huynh trên https://tailieugiaovien.com.vn/ . Hỗ trợ zalo Viet
Jack Official
Doc.com KHÔNG quảng cáo, với tải file cực nhanh không ngóng đợi.
Chuyên đề luyện thi vào 10: Tìm quý hiếm của x nhằm biểu thức nhận giá trị nguyên
I. Bí quyết tìm quý giá của x để biểu thức nguyênTìm quý hiếm của x nhằm biểu thức nhận giá trị nguyên là dạng bài bác thường xuất hiện thêm trong những đề thi Toán lớp 9 cũng như tuyển sinh vào lớp 10. Để giúp những em học viên nắm vững vàng dạng Toán này, Vn
Doc nhờ cất hộ tới chúng ta tài liệu Tìm quý giá x nguyên để A nhận quý hiếm nguyên, kèm lấy ví dụ minh họa và bài bác tập trường đoản cú luyện. Tư liệu này để giúp các em làm cho quen với các dạng bài bác tập kiếm tìm x, từ đó nâng cấp kỹ năng giải bài xích để chuẩn bị tốt mang lại kì thi vào lớp 10 sắp tới. Dưới đó là nội dung chi tiết, mời các em cùng tìm hiểu thêm nhé.
I. Bí quyết tìm quý hiếm của x để biểu thức nguyên
1. Dạng 1: Tìm giá trị nguyên của x nhằm biểu thức A nhận quý giá nguyên
+ thông thường biểu thức A sẽ sở hữu được dạng

+ cách làm:
- cách 1: tách bóc về dạng

- cách 2: Để A nhận quý giá nguyên thì


- cách 3: Lập bảng nhằm tính những giá trị của x
- cách 4: Kết hợp với điều kiện đề bài, loại trừ những giá trị không phù hợp, tiếp nối kết luận bài bác toán
2. Dạng 2: Tìm quý giá của x để biểu thức A nhận quý hiếm nguyên
+ Đây là một trong những dạng cải thiện hơn của dạng bài bác tập tìm gá trị nguyên của x để biểu thức A nhận cực hiếm nguyên vị ta chưa xác minh giá trị của vươn lên là x có nguyên hay là không để đổi khác biểu thức A về dạng

- bước 1: Áp dụng điều kiện cùng với những bất đẳng thức vẫn được, chứng tỏ m
Vậy cùng với x ∈ - 1; 0; 2; 3 thì biểu thức

b,

Ta có:

Để


Ta tất cả bảng:
| x - 1 | -1 | 1 |
| x | 0 (thỏa mãn) | 2 |
Vậy với x ∈ 0; 2 thì biểu thức

c,

%20-%203%7D%7D%7B%7B%5Csqrt%20x%20%20%2B%201%7D%7D%20%3D%20%5Cfrac%7B%7B3%5Cleft(%20%7B%5Csqrt%20x%20%20%2B%201%7D%20%5Cright)%7D%7D%7B%7B%5Csqrt%20x%20%20%2B%201%7D%7D%20-%20%5Cfrac%7B3%7D%7B%7B%5Csqrt%20x%20%20%2B%201%7D%7D%20%3D%203%20-%20%5Cfrac%7B3%7D%7B%7B%5Csqrt%20x%20%20%2B%201%7D%7D)
Để


Ta có bảng:
 | -3 | -1 | 1 | 3 |
 | -4 (loại) | -2 (loại) | 0 | 2 |
| x | 0 (thỏa mãn) | 4 (thỏa mãn) |
Vậy với x ∈ 0; 4 thì biểu thức

Bài 2: Tìm giá trị của x để những biểu thức tiếp sau đây nhận quý giá nguyên
a,


Lời giải:
Bài toán trực thuộc vào dạng 2: tìm các giá trị của x để biểu thức nhận quý hiếm nguyên. Giải pháp làm cụ thể cho từng bài xích như sau:
a,

Có

Lại bao gồm

Áp dụng bất đẳng thức Cauchy mang lại



Từ (1) với (2) ta có:


Giải phương trình tính được x = 0
Vậy với x = 0 thì biểu thức nhận giá trị nguyên
b,

Có

Lại bao gồm

Áp dụng bất đẳng thức Cauchy mang lại


Từ (1) va (2) ta bao gồm


Vậy cùng với x = 0 thì biểu thức nhận giá trị nguyên
Bài 3: đến biểu thức

a) Rút gọn gàng biểu thức A.
b) Tìm các số nguyên x nhằm M = A. B đạt quý giá nguyên.
Lời giải:
a) Rút gọn biểu thức ta được kết quả:

b) Ta có:

a) Rút gọn biểu thức A.
b) Tìm giá trị của x nhằm A nhận giá trị là số nguyên.
Lời giải:
a) học viên thực hiện tại rút gọn gàng biểu thức, ta tất cả kết quả:

b) học viên tham khảo một trong những cách có tác dụng dưới đây:
Cách 1: cùng với

Vậy 0 x = 1 (Không thỏa mãn)
Vậy không có giá trị nguyên như thế nào của x để quý hiếm A là một số trong những nguyên.
Cách 2: cần sử dụng miền giá bán trị
%5Csqrt%20x%20%20%2B%20A%20-%202%20%3D%200)
Trường hợp 1: giả dụ A = 0

Trường thích hợp 2: trường hợp A không giống 0

Với A = 1 => x = 1 (Loại)
Với A = 2

Vậy không có giá trị nguyên như thế nào của x để cực hiếm A là một số trong những nguyên.
III. Bài tập trường đoản cú luyện tìm cực hiếm của x để biểu thức có mức giá trị nguyên
Bài 1: Tìm những giá trị nguyên của x để biểu thức dưới đây nhận quý giá nguyên








